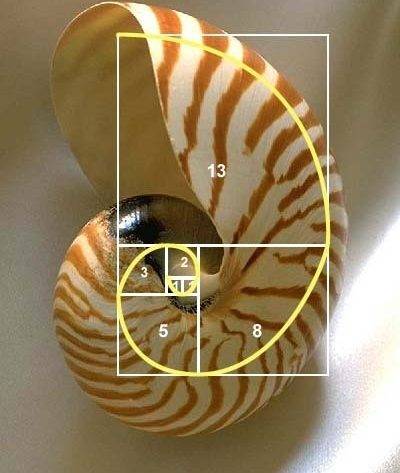
在13世紀末出生的意大利數學家Leonardo Fibonacci發現黃金比率,是由一系列的神奇數字計算而成, 包括1、1、2、3、5、8、13、21、34、55、89、144、233、377……任何一個數字都是前面兩數字的總和: 2=1+1、3=2+1、5=3+2、8=5+3……,如此類推。 市場一直不會一直上升,一直下跌。而是分波段的運動,即如波浪理論中對股市描述,股市的完整結構是以五個上升波和三個下降波構成。而波段中的中存在黃金比率的關係。為了了解市場的擴張及收縮,必須了解黃金比率。 1202年,義大利數學家斐波那契出版了他的「算盤全書」。他在書中提出了一個關於兔子繁殖的問題: 如果一對兔子每月能生一對小兔(一雄一雌),而每對小兔在牠出生後的第三個月裡,又能開始生一對小兔,假定在不發生死亡的情況下,由一對出生的小兔開始,50個月後會有多少對兔子?
在13世紀末出生的意大利數學家Leonardo Fibonacci發現黃金比率,是由一系列的神奇數字計算而成, 包括1、1、2、3、5、8、13、21、34、55、89、144、233、377……任何一個數字都是前面兩數字的總和: 2=1+1、3=2+1、5=3+2、8=5+3……,如此類推。 市場一直不會一直上升,一直下跌。而是分波段的運動,即如波浪理論中對股市描述,股市的完整結構是以五個上升波和三個下降波構成。而波段中的中存在黃金比率的關係。為了了解市場的擴張及收縮,必須了解黃金比率。 1202年,義大利數學家斐波那契出版了他的「算盤全書」。他在書中提出了一個關於兔子繁殖的問題: 如果一對兔子每月能生一對小兔(一雄一雌),而每對小兔在牠出生後的第三個月裡,又能開始生一對小兔,假定在不發生死亡的情況下,由一對出生的小兔開始,50個月後會有多少對兔子?
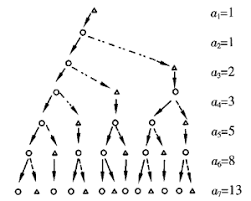
在第一個月時,只有一對小兔子,過了一個月,那對兔子成熟了,在第三個月時便生下一對小兔子,這時有兩對兔子。再過多一個月,成熟的兔子再生一對小兔子,而另一對小兔子長大,有三對小兔子。由此可知,從第一個月開始以後每個月的兔子總數是: 1,1,2,3,5,8,13,21,34,55,89,144,233…若把上述數列繼續寫下去,得到的數列便稱為斐波那契數列。數列中每個數便是前兩個數之和,而數列的最初兩個數都是1。若設 F0=1, F1=1, F2=2, F3=3, F4=5, F5=8, F6=13… 則:當n>1時,Fn+2 = Fn+1 + Fn,而 F0=F1=1。下面斐波那契數列的式子: 斐波那契數列數式 於是費波那契Leonardo Fibonacci) 現的一連串的數位,它們是 0、1、1、2、3、5、8、13、21、34、55、89、144、610、754…等,每個接連的數字都是由前兩個數字相加而成的。該數列最吸引人之處在於隨數列向無窮大發展數列中始終存在一常數:你會發現兩個相鄰數字間的比率總是約為1.618。例如,用後一個數位除去前一個數位時,所得出的答案大約等於0.618。(21/34 = 0.617647),與黃金比率有關。如將144除以89,即得出1.618。因此我們就知道1.618是非常要。
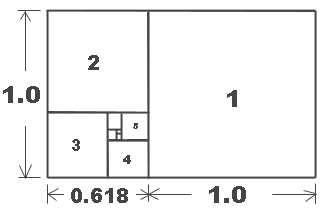
我們常見的黃金比率為0,0.236,0.382,0.618,0.786及1,此外,亦會用到1.382,1.618等數值。黃金數字間亦互有關係,如兩個重要的黃金數字0.618及0.382,兩者相加為1,即1-0.618=0.382,所以可以利用同理將1-0.236=0.764。同樣地,亦可將0.382乘2得出0.764。此外,將0.618除以0.382亦可得出另一個黃金數字1.618或將 1.618除以0.618得出2.618。

菲波納奇這個名稱你可能有些陌生,但如果你看過影片 《達 ·芬奇密碼 》,就一定會對它有些印象。達芬奇名畫 《維特魯威人 》 的姿勢。 這幅畫解釋了菲波納奇比率與人體結構的關係。 有人說這些數字是他從研究金字塔所得出。金字塔和上列奇異數字息息相關。金字塔的幾何形狀有五個面,八個邊,總數為十三個層面。由任何一邊看進去,都可以看到三個層面。金字塔的長度為5813寸(5-8-13),而高底和底面百分比率是0.618,那即是上述神秘數字的任何兩個連續的比率,譬如55/89=0.618,89/144=0.618,144/233=0.618。 另外,一個金字塔五角塔的任何一邊長度都等於這個五角型對角線(Diagonal)的0.618。還有,底部四個邊的總數是36524.22寸,這個數字等於光年的一百倍!
這組數字十分有趣。0.618的倒數是1.618。譬如14/89=1.618、233/144=1.618,而0.618×1.618=1,就等於1。 另外有人研究過向日葵,發現向日葵花有89個花辮,55個朝一方,34個朝向另一方。 神秘?不錯,這組數字就叫做神秘數字。而0.618,1.618就叫做黃金分割率(Golden Section)。 2.黃金分割率的特點 黃金分割率的最基本公式,是將1分割為0.618和0.382,它們有如下一些特點: (1)數列中任一數字都是由前兩個數字之和構成。 (2)前一數字與後一數字之比例,趨近於一固定常數,即0.618。 (3)後一數字與前一數字之比例,趨近於1.618。 (4)1.618與0.618互為倒數,其乘積則約等於1。 (5)任一數字如與後兩數字相比,其值趨近於2.618;如與前兩數字相比,其值則趨近於0.382。 理順下來,上列奇異數字組合除能反映黃金分割的兩個基本比值0.618和0.382以外,尚存在下列兩組神秘比值。即: (1) 0.191、0.382、0.5、0.618、0.809 (2)1、1.382、1.5、1.618、2、2.382、2.618 0.382÷2=0.191 1-0.618=0.382 2.618х0.618=1.618 0.618 х0.618=0.382 2.618 х0.382=1 1.618х1.618=2.618 斐波那契數列一種與黃金比例同等理想的數 列。具規則的平穩性,越後面越接近黃金比。而這個比例就是「黃金比例」。換句話說,「斐波那契數列」會產生出「黃金比例」。

地球上大部份生命的構造,運行之間軌跡或藝術品的設計都是有一定黃金比率的關係。如向日葵種子的生長螺紋是左旋和右旋的兩組交錯等角螺線,右 21道與左旋 34 道,1:1.619 趨近黃金比例。也有較大的向日葵,左旋數和右旋數各為 34 和 55,更大的向日葵則有 89 和 144,甚至 144和 233 的排列數,大多數所熟識藝術品其實也與斐波納契數列有關。假如在一系列長方形中挑選出最為美觀的長方形,多數人會選擇兩邊比例(即長÷闊)約1.62的長方形4,即長度是闊度的1.62倍。著名古希臘建築帕台農神殿,其正面勾勒出一個長方形,兩邊長度便是根據這「黃金比例」。「黃金比例」在藝術和建築學上獲得廣泛應用。如古埃及的金字塔大小雖有不同,但是金字塔底面的邊長與高的比率都接近於0.618。而近代著名的法國巴黎埃費爾鐵塔,其第二層以下和第二層以上的高度比率是0.618。派特農神廟,也是建築中運用黃金分割的典例。 3.黃金分割率在投資中的運用 在股價預測中,根據該兩組黃金比有兩種黃金分割分析方法。
第一種方法:以股價近期走勢中重要的峰位或底位,即重要的高點或低點為計算測量未來走勢的基礎,當股價上漲時,以底位股價為基數,跌幅在達到某一黃金比時較可能受到支撐。當行情接近尾聲,股價發生急升或急跌後,其漲跌幅達到某一重要黃金比時,則可能發生轉勢。第二種方法:行情發生轉勢後,無論是止跌轉升的反轉抑或止升轉跌的反轉,以近期走勢中重要的峰位和底位之間的漲額作為計量的基數,將原漲跌幅按0.382、0.5、0.618分割。股價在後轉後的走勢將有可能在這些黃金點上遇到暫時的阻力或支撐。 舉例:當下跌行情結束前,某股的最低價10元,那麼,股價反轉上升時,投資人可以預先計算出各種不同的反壓價位,也主不是,1X(1+38.2%)=13.8,1×(1+61.8%)=16.2元,10×(1+100%)=20元,10+(1+119.1%)=21.9元,然後,再依照實際股價變動情形做斟酌。 反之上升行情結束前,某股最高價為30元,那麼,股價反轉下跌時,投資人也可以計算出各種不同的持價位,也就是,30×(1-38.2%)=18.5元,30×(1-61.8%)=11.5元,。然後,依照實際變動情形做斟酌。 本文章節錄於「江恩周期與和諧交易」一書
 ]]>
]]>